2 آذر 1401
زمان مطالعه: 14 دقیقه

آشنایی با سوگیری بازماندگی؛ سراب موفقیت!

تیم محصول

نوشته شده توسط

جلیل علیزاده

تسلط بر مباحث آماری و تحلیل داده یکی از مهارت‌های مهمی است که مدیران محصول نسل جدید، باید به آن مسلط باشند. در این مقاله به سراغ یکی از مباحث جذاب علم آمار می‌رویم و یکی از خطاهای متداول استدلالی و آماری را بررسی می‌کنیم که همان «سوگیری بازماندگی» یا Survivorship bias است. این خطای استدلالی زمانی رخ می‌دهد که فرد بخواهد با مشاهده و بررسی تعداد محدودی از نمونه‌ها به یک نتیجه‌گیری کلی برسد. تسلط بر این مبحث و آشنایی با آن برای یک مدیر محصول ضروری است، چراکه اساساً یکی از مهم‌ترین کارهای یک مدیر محصول تصمیم‌گیری است. یک تصمیم‌گیری صحیح می‌تواند منابع مختلفی داشته باشد که قطعاً یکی از مهم‌ترین آن‌ها «داده» است؛ بنابراین تسلط بر نحوه استفاده از داده و طی‌کردن فرایند صحیح نتیجه‌گیری اهمیت فراوانی دارد.

نگاه اولیه به سوگیری بازماندگی (Survivorship bias)

سوگیری بازماندگی یا سوگیری بقا یک خطا در فرایند نتیجه‌گیری (استدلال) منطقی است. این خطا نتیجه تمرکز روی داده‌هایی از فضای نمونه است که از یک فرایند خاص عبور کرده‌اند و نادیده‌گرفتن اعضایی از فضای نمونه است که از آن فرایند خاص گذر نکرده‌اند یا به هر دلیلی به چشم نمی‌آیند و اطلاعاتی از آنان در دسترس نیست.

در بیشتر موارد رخ‌دادن مدل سوگیری (Bias) تنها نمونه‌های زنده یا موفق مورد بررسی قرار می‌گیرند و همین امر باعث اشتباه در داوری یا نتیجه‌گیری می‌شود. سوگیری بازماندگی معمولاً باعث ایجاد نتیجه‌گیری‌های بیش از حد خوش‌بینانه و موفقیت‌آمیز می‌شود، چراکه در این نتیجه‌گیری شکست‌های متعدد نادیده گرفته شده است. به طور مثال از یک دبیرستان، ۵ نفر موفق به تحصیل در رشته مهندسی برق دانشگاه صنعتی شریف می‌شوند. اگر داده‌های ما تنها محدود به نمونه‌های موفق باشد، در نگاه اول ممکن است نتیجه‌گیری کنیم که این دبیرستان احتمالاً کیفیت آموزشی بسیار بالایی داشته است. اما اگر کل فضای نمونه را بررسی کنیم و متوجه شویم که به طور مثال از ۱۰۰ نفر دانش‌آموز این دبیرستان، ۲۰ نفر حتی مجاز به انتخاب رشته نشده‌اند و به جز آن ۵ نفر کسی موفق به قبولی در شهر تهران نشده است؛ بدین ترتیب با دانستن این اطلاعات نظرمان در ارتباط با اینکه آن دبیرستان کیفیت آموزشی ارزنده‌ای داشته است، تغییر می‌کند! این یک مثال ساده از بحث «سوگیری بازماندگی» بود. در ادامه این مقاله به بررسی عمیق چند مثال از این سوگیری در فضاهای مختلف می‌پردازیم.

جنگ جهانی دوم و بمباران هوایی

در جنگ جهانی دوم بمباران هوایی آلمان یکی از ابزارهای اصلی متفقین برای ضربه‌زدن به کشور آلمان بود. در این میان نیروی هوایی بریتانیا تحقیقات ویژه‌ای را به‌منظور مقاوم‌سازی هواپیماهای جنگی خود آغاز کرده بود. مشکل اصلی این بود که در طی بمباران هوایی آلمان، تجهیزات هواپیمایی بریتانیا متحمل آسیب شدیدی شده بود و در یک بازه زمانی، شانس بازگشت یک هواپیما از مأموریت چیزی کمتر از ۵۰ درصد بود و همین امر علاوه بر اینکه باعث ازبین‌رفتن خدمه هوایی، تجهیزات نظامی و منابع وسیع مالی می‌شد، انگیزه و روحیه پرسنل نیروی هوایی را نیز به طور محسوسی کاهش داده بود، چراکه شانس زنده ماندن آن‌ها از هر مأموریت بسیار پایین بود.

به همین منظور رهبران نظامی بریتانیا تصمیم گرفتند تا با افزودن زره به هواپیماها مقاومت آن را افزایش دهند، اما با یک مشکل بزرگ روبه‌رو بودند؛ افزودن زره به تمام قسمت‌های هواپیما امکان‌پذیر نبود، چراکه باعث سنگین شدن بیش از حد هواپیما می‌شد و پرواز را مشکل می‌کرد. مسئله‌ای که نیروی هوایی بریتانیا با آن روبه‌رو بود به معنای واقعی کلمه یک چالش محصولی بود. در نهایت تصمیم بر آن شد که زره تنها به قسمتی از هواپیما اضافه شود که بیشتر از دیگر قسمت‌ها مورد اصابت گلوله قرار گرفته است. پس از این تصمیم‌گیری تحقیقات روی هواپیماها با کمک ارتش آمریکا انجام شد و با تحلیل و بررسی صدها نمونه هواپیما طرحی شبیه به شکل زیر به دست آمد.

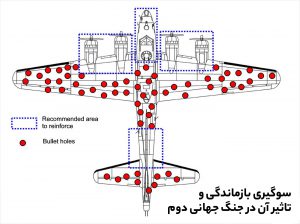
نقاط مشخص شده، بیشترین گلوله را دریافت کرده بودند، بنابراین تصمیم بر آن شد که به این نقاط زره بیشتری اضافه شود تا مقاومتشان افزایش یابد. پس از انجام این کار انتظار می‌رفت که طول عمر هواپیماها و نرخ بازگشت از مأموریت افزایش یابد، اما پس از گذشت مدتی تغییر محسوسی حاصل نشد. بدین ترتیب نیروی هوایی بریتانیا تیم جدید تحقیقاتی به رهبری «آبراهام وایلد» را مسئول بررسی این پروژه کرد. آبراهام وایلد پس از مدتی بررسی نمونه‌های قابل‌دسترس نظر عجیبی را مطرح کرد. نظریه او این بود که مقاوم‌سازی و زره‌ها باید به نقاطی اضافه شود که اصلاً تیر نخورده‌اند. استدلال او این بود که این تحقیقات روی هواپیماهایی انجام‌گرفته است که بازگشته‌اند؛ یعنی از مأموریت جان سالم به در برده‌اند، بنابراین احتمالاً نقاطی که تیر نخورده‌اند، دقیقاً همان نقاط حساس هواپیما هستند که وقتی تیر به آن‌ها برخورد کند، هواپیما سقوط می‌کند و دیگر امکان بررسی آن وجود ندارد. این نظریه وایلد در آن زمان انقلابی در زمینه توسعه «سوگیری بازماندگی» محسوب می‌شد و سبب افزایش سرعت پیشرفت این نظریه شد.

با افزودن زره به بخش‌هایی که تیر نخورده بودند، نرخ بازگشت و طول عمر هواپیماها افزایش چشمگیری داشت و کمک شایانی به افزایش توانمندی نیروی هواپیمایی بریتانیا در مقابله با آلمان نازی کرد. در بخش پایانی این مقاله نگاه عمیق‌تری به کارهای پژوهشی وایلد می‌اندازیم و با استفاده از روابط ریاضی و آماری به بررسی نتیجه‌گیری او می‌پردازیم.

فروش موفقیت و نوابغ پوشالی!

یکی از موضوعاتی که احتمالاً شما هم درباره آن زیاد شنیده‌اید و رسانه‌ها نیز علاقه وافری به مانور دادن روی آن دارند، بررسی افرادی است که به دانشگاه نرفته یا ترک تحصیل‌کرده‌اند و در دنیای کسب‌وکار بسیار موفق هستند. این موضوع به‌قدری در سال‌های اخیر همه‌گیر شده است که عده‌ای گمان می‌کنند که برای موفقیت و میلیارد شدن باید از دانشگاه و فضای آکادمیک فرار کرد. باتوجه‌به مناقشه‌انگیز بودن این موضوع، رسانه‌ها نیز علاقه زیادی به تولید محتوا درباره آن دارند و هرازگاهی شاهد این هستیم که مقالاتی نظیر؛ «۱۵ میلیاردر که ترک تحصیل کردند»، «آیا شما واقعاً به دانشگاه نیاز دارید؟» و … منتشر می‌شود و در اکثر این مقالات نیز به اسامی «استیو جابز»، «بیل گیتس»، «مارک زاکربرگ»، «مایکل دل» و … اشاره می‌شود. بدین ترتیب این حس در غالب افراد ایجاد می‌شود که احتمالاً دانشگاه و تحصیلات آکادمیک یک فرایند زاید است و با ترک کردن آن می‌توان به موفقیت‌های هیجان‌انگیزی دست پیدا کرد. اما آیا این تمام واقعیت است؟

بدیهی است که پاسخ این سؤال منفی است و اکثر این مقالات و محتواها صرفاً یک جوسازی رسانه‌ای بدون پشتوانه است. غالب رسانه‌ها با تولید چنین محتوایی یک سؤال و ابهام برای مخاطبان خود ایجاد می‌کنند، سپس برای برطرف‌کردن این ابهام کاذب، شروع به فروش کتاب، سمینار، محتوای ویدئویی و … می‌کنند که در آن قرار است به شما راه واقعی موفقیت و پول‌دار شدن را بیاموزد!

اتفاقی که در اینجا رخ‌داده است دقیقاً یک مدل از «سوگیری بازماندگی» است. چراکه در این استدلال تنها افرادی مورد بررسی قرار گرفته‌اند که پس از ترک تحصیل توانسته‌اند یک موفقیت قابل‌توجه کسب کنند. در این مدل استدلال میلیون‌ها نفری که پس از ترک تحصیل دچار مشکلات جدی مالی و کاری شده‌اند مورد بررسی قرار نگرفته است و تنها مبتنی بر چند داده محدود، فرایند نتیجه‌گیری رخ‌داده است. اساس این مدل استدلال یک ایراد جدی دارد، آن هم بازخوانی تاریخ به شکلی است که مخاطب احساس می‌کند یک پیش‌بینی رخ می‌دهد!

در حالت کلی احتمال اینکه یک فرد ترک تحصیل‌کرده مدیرعامل اپل شود؛ ۱ در ۱۰ میلیون است. اما وقتی یک فرد تبدیل به مدیرعامل اپل شد، احتمال مدیرعامل شدن او ۱۰۰ درصد است، چون اساساً این پدیده رخ‌داده است؛ بنابراین اگر شخصی پیش‌بینی کرد که فلان فرد ترک تحصیل‌کرده، به‌زودی مدیرعامل اپل خواهد شد و این اتفاق رخ داد، بسیار قابل‌توجه و پراهمیت است. اما بررسی کردن پدیده پس از آن که فرد مدیرعامل اپل شد، باعث درگیر شدن با خطای منطقی «سوگیری بازماندگی» می‌شود.

برای فهم بهتر این موضوع، بهتر است چند آمار و ارقام را با هم بررسی می‌کنیم. باتوجه‌به آمارهایی که در آمریکا منتشر شده است، میانگین درآمد سالیانه افرادی که تحصیلات دانشگاهی دارند ۵۳ هزار دلار است، این در حالی است که میانگین درآمد افرادی که ترک تحصیل‌کرده‌اند یا وارد دانشگاه نشده‌اند تنها ۲۷ هزار دلار است. این سخن بدین معنا است که یک نمونه تصادفی از جامعه دارای تحصیلات دانشگاهی به‌احتمال زیاد بیشتر از ۲ برابر یک نمونه تصادفی از جامعه فاقد تحصیلات دانشگاهی، درآمد دارد و این دقیقاً چیزی است که رسانه هیچ‌گاه به شما نمی‌گوید، چراکه دوست دارد به شما آرزو فروشی کند و بابت ارائه فرمول مهمل موفقیت و یک‌شبه میلیاردر شدن، درآمد هنگفتی کسب کند!

برای درک بهتر این موضوع با تفکیک بیشتری جامعه افراد دارای تحصیلات دانشگاهی و فاقد تحصیلات دانشگاهی را بررسی می‌کنیم. در پژوهشی که دانشگاه Northeastern در آمریکا انجام داده است، میانگین درآمد سالیانه افراد به تفکیک مدرک دانشگاهی آنان محاسبه شده است. این پژوهش نشان می‌دهد که افراد با درجه PHD یا همان دکترای تخصصی، به طور میانگین سالیانه ۹۸ هزار دلار درآمد دارند و نرخ بیکاری در این گروه ۱.۱ درصد است. این در حالی است که میانگین درآمد سالیانه افرادی که تنها تحصیلات دبیرستان را گذرانده و به دانشگاه نرفته‌اند، نزدیک به ۳۹ هزار دلار است و نرخ بیکاری در این گروه ۳۷ درصد است. این سخن بدین معنا است که یک نمونه تصادفی از جامعه افرادی که مدرک دکترای تخصصی دارند به طور میانگین ۲.۵ برابر افرادی که تنها تا پایان دبیرستان تحصیل‌کرده‌اند، درآمد دارند و احتمال بیکار ماندن این افراد نسبت به دسته دوم ۷۰ درصد کمتر است؛ بنابراین واضح است که آمار و ارقام به ما می‌گوید که تحصیلات دانشگاهی بالاتر، احتمال موفقیت کاری و کسب درآمد بیشتر شما را به طور قابل‌توجهی افزایش می‌دهد.

مدیریت محصول و فرار از سوگیری بازماندگی

یکی از مهم‌ترین کارهایی که یک مدیر محصول موظف به انجام آن است، انجام دقیق و صحیح فرایند «کشف ویژگی» یا همان Feature Discovery برای محصول است. در این فرایند مشخص می‌شود که قابلیت‌های جدید محصول چه خواهد بود و بدین ترتیب محصول همواره متناسب با نیاز بازار توسعه داده می‌شود.

فرایند Feature Discovery به‌نوعی ضامن حیات یک محصول خواهد بود، چراکه اگر این فرایند به‌درستی انجام نشود و قابلیت‌هایی توسعه داده شود که متناسب با نیاز بازار و کاربران نباشد، از طرفی حجم زیادی سرمایه مالی که بابت توسعه محصول هزینه شده است، از بین می‌رود و از سوی دیگر کاربران محصول ریزش خواهند کرد و باید تلاش مجددی جهت بازگرداندن آنان انجام شود؛ بنابراین بسیار مهم است که این فرایند Feature Discovery، «داده‌محور» و مبتنی بر نیازمندی‌های کاربران انجام شود.

یکی از اتفاقات متداولی که برای مدیران محصول رخ می‌دهد، این است که آنان برای تصمیم‌گیری در مورد قابلیت‌های جدید محصول خود تنها به نظرات کاربران فعلی اتکا می‌کنند و سوگیری بسیار شدیدی به بازخوردهای کاربران فعال محصول دارند. این رویکرد باعث می‌شود که شما در تله «سوگیری بازماندگی» گرفتار شوید و این موضوع مانع رشد محصول و افزایش کاربر شما خواهد شد و در بهترین حالت محصول شما سیر ثابتی را طی خواهد کرد. احتمالاً اکنون این سؤال پیش می‌آید که پس چه‌کار باید کرد و به بازخوردهای کدام دسته از کاربران توجه بیشتری کرد؟

از نظر نگارنده (جلیل علیزاده) در فرایند Feature Discovery مهم‌ترین نگاه مدیر محصول باید به سمت افرادی باشد که اکنون کاربر او نیستند یا دچار ریزش شده‌اند. بازخوردهای این افراد دقیقا نشان می‌دهد که محصول شما کدام ویژگی‌ها و قابلیت‌های حیاتی را نداشته است و این خلأ چه احساسی را در مخاطب ایجاد کرده که باعث شده دیگر از محصول استفاده نکند؛ بنابراین نیاز است که با تحلیل داده‌های محصول، بررسی نیازهای بازار و برگزاری جلسات مصاحبه با کاربران ریزش شده، حفره‌های محصول را پیدا کرد و با پوشش آنان بقای محصول را تضمین کرد.

بار دیگر به مثال هواپیماهای جنگی جنگ جهانی دوم باز گردیم و فضای آنجا را به فضای مدیریت محصول شبیه‌سازی کنیم. در اینجا کاربران فعلی شما، آثار گلوله‌هایی هستند که در بدنه‌ هواپیماهای فعلی به‌جای مانده‌اند و کاربران ریزش شده دقیقاً همان نقاطی هستند که در نگاه اول تیری به آنان برخورد نکرده است؛ بنابراین واضح است که نیازمندی‌های کاربران ریزش شده، اولویت بسیار بالاتری نسبت به نیازمندی‌های کاربران فعلی دارد، چراکه آن نیازمندی‌ها، دقیقاً همان مواردی بوده‌اند که باعث شده‌اند کاربر دیگر از محصول شما استفاده نکند و احتمالاً به دنبال یک جایگزین باشد.

بنابراین اگر یک مدیر محصول هستید، حتماً کاربران ریزش شده را جدی بگیرید، البته که ارتباط با این دسته از افراد بسیار سخت‌تر است، چراکه این دسته از افراد اساساً محصول شما را دوست ندارند و قطعاً بازخوردهای خوشحال‌کننده و سرشار از محبتی را به شما نخواهند داد، اما در پَس نکات سخت آنان، مواردی است که به شما هشدار می‌دهد که محصول شما چه پرتگاه‌های خطرناکی دارد.

اکنون ممکن است این سؤال پیش بیاید که چه زمانی باید به بازخوردهای کاربران فعلی توجه کرد و نکات آنان را در توسعه محصول مدنظر قرار داد؟ در پاسخ به این سؤال می‌توان متغیرهای مختلفی را مدنظر قرار داد و بدیهی است که جواب ۱۰۰ درصد دقیق و قطعی به آن وجود ندارد، در این جا ما دو سناریو را بررسی می‌کنیم. در این دو سناریو، بازخوردهای کاربران فعلی شما اهمیت بسیار بالاتری نسبت به کاربران ریزش شده دارد.

پیاده‌سازی استراتژی «آپ سلینگ»

به‌طورکلی فرایند آپ سلینگ (Upselling) منجر به این می‌شود که کاربران فعلی شما، محصول گران‌قیمت‌تری را از شما خریداری کنند و در این فرایند یک اتفاق برد – برد میان کاربر و فروشنده اتفاق می‌افتد، یعنی هم سود بیشتری عاید کسب‌وکار می‌شود و هم خریدار از امکانات و قابلیت‌های بیشتری برخوردار می‌شود.

آمارها حاکی از آن است که فروش یک محصول به مشتری فعلی کسب‌وکار، ۵ برابر آسان‌تر از فروش آن به فردی است که مشتری شما نیست؛ بنابراین اگر در استراتژی کسب‌وکار خود محصول یا قابلیت جدیدی را به سبد محصولات خود اضافه کرده‌اید که گران‌تر است و قصد فروش آن را دارید، پیشنهاد می‌کنیم که در این برهه زمانی نیازمندی‌های کاربران فعال محصول خود را جدی بگیرید تا بتوانید محصول جدید و گران‌قیمت‌تر خود را با سهولت بیشتری عرضه و به فروش برسانید.

کاهش ریسک یا اشباع بازار هدف

در بعضی از کسب‌وکارها راضی نگه‌داشتن مشتری فعلی اهمیت بسیار ویژه‌ای دارد. تصور کنید شما یک کسب‌وکار Saas هستید و اکنون نزدیک به پایان موعد قرارداد سالیانه شما با مشتری است. بدیهی است که فرایند تمدید کردن قرارداد مشتری فعلی، کار بسیار ساده‌تری نسبت به عقد قرارداد با یک مشتری جدید است؛ بنابراین شما باید سعی کنید که نیازمندی‌های مشتری فعلی را به‌صورت کامل در نظر بگیرید و با ایجاد قابلیت‌هایی که بخشی از این نیازها را برطرف می‌کند، این حس را در مشتری خود ایجاد کنید که تجربه کاربری او برای کسب‌وکار شما اهمیت ویژه‌ای دارد و بدین ترتیب او احتمالاً به‌راحتی قرارداد با شما را تمدید خواهد کرد و درآمد شما ادامه‌دار خواهد بود.

در بعضی مواقع نیز کسب‌وکار شما به‌قدری موفق عمل کرده است که بازار را اشباع کرده‌اید. به طور مثال یک کسب‌وکار تاکسی اینترنتی هستید و ۸۰ درصد از سهم بازار را مال خود کرده‌اید. در چنین شرایطی حفظ مشتریان فعلی اهمیت چند برابری نسبت به جذب مشتریان ریزش شده دارد، چراکه باتوجه‌به سهم بازار بالای شما، احتمالاً رقبایی خواهید داشت (که اکثرا تیم کوچک‌تر و چابک‌تری نسبت به شما دارد) که آماده‌اند با کوچک‌ترین خطای سازمان شما یک مشتری ناراضی شما را جذب کنند و بخشی از سهم بازار شما را مال خود کنند.

مروری بر کارهای پژوهشی وایلد و توسعه مفهوم سوگیری شناختی

همان‌طور که در بخش‌های قبلی مقاله اشاره کردیم، «اضافه کردن زره به قسمت‌هایی از هواپیما به منظور افزایش طول‌عمر آن‌ها در حین عملیات نظامی» مسئله اصلی ناوگان هوایی بریتانیا بود و تیم آبراهام وایلد مسئولیت حل این مسئله را برعهده گرفته بود.

راهکار وایلد در گام اول برای حل مسئله این بود که نحوه توزیع گلوله‌ها روی هواپیماهای بازگشتی را بررسی کند و سپس با ایجاد یک فرمول‌بندی به این نتیجه برسد که کدام بخش‌های هواپیما در مقابل گلوله آسیب‌پذیرتر است و به آن بخش‌ها پوشش محافظتی اضافه کند. البته لازم به ذکر است که تحقیقات وایلد تنها روی هواپیماهایی انجام می‌شد که از ماموریت بازگشته بودند و اطلاعاتی از هواپیماهای سقوط کرده وجود نداشت.

با توجه به عدم دسترسی به داده‌های هواپیماهای سقوط کرده، وایلد سعی کرد مسئله را به بخش‌های کوچک‌تری تقسیم و این چنین حل کند:

- اگر به یک هواپیما تعداد 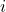$i$ گلوله برخورد کند، با چه احتمالی پس از برخورد $i+1$ گلوله می‌تواند به پرواز ادامه دهد؟

- اگر به یک قسمت خاص از هواپیما گلوله برخورد کند، احتمال ادامه پرواز هواپیما چقدر می‌شود؟

در گام بعدی، وایلد سعی کرد راهکار خود را برای یک نمونه عددی پیاده‌سازی کند.

فرض کنیم 400 هواپیما به ماموریت فرستاده شده‌اند و تعداد هواپیماهای بازگشتی که تعداد $i$ گلوله به آن‌ها برخورد کرده است که آن را $A_i$ تعریف می‌کنیم، عبارت است از:

$\boldsymbol{A_0=320}$ , $\boldsymbol{A_1=32}$ , $\boldsymbol{A_2=20}$ , $\boldsymbol{A_3=4}$ , $\boldsymbol{A_4=2}$ , $\boldsymbol{A_5=2}$

به‌طور مثال $A_1=32$ بدین معنا است که تعداد هواپیماهای بازگشتی که ۱ گلوله به آن‌ها اصابت کرده است، برابر با ۳۲ است. بنابراین از اطلاعات فوق به راحتی می‌توان متوجه شد که از ۴۰۰ هواپیمایی که به ماموریت رفته بودند، ۳۸۰ هواپیما بازگشته‌اند و اطلاعاتی از ۲۰ هواپیما در دسترس نیست.

اکنون که مشخص کردیم به هواپیماهای بازگشتی به تفکیک چند گلوله اصابت کرده است، به بررسی این موضوع می‌پردازیم که هر گلوله به کدام بخش‌های هواپیما برخورد کرده است. به طور کلی هر هواپیما را به چهار قسمت تقسیم می‌کنیم:

1. موتورها
2. بدنه هواپیما
3. سیستم سوخت‌رسانی هواپیما
4. سایر قسمت‌ها

همچنین مقدار $\gamma(i)$ را معادل مساحت اشغالی بخش $i$ تقسیم بر مساحت کل تعریف می‌کنیم (در حقیقت $\gamma(i)$ احتمال عمومی برخورد گلوله با آن بخش از هواپیما است) و همچنین $N(i)$ را معادل تعداد گلوله‌هایی که به بخش $i$ اصابت کرده است، تعریف می‌کنیم. در شرایط فعلی مقدار کل گلوله‌های اصابت شده برابر $\sum_{n=1}^{5}=iA_i=102$ است، بدین ترتیب به تفکیک خواهیم داشت:

در گام بعدی مقدار $\delta(i)$ را برابر نسبت برخورد گلوله به قسمت $i$ به کل گلوله‌های اصابت شده قرار می‌دهیم، بدین ترتیب خواهیم داشت:

$\boldsymbol{\delta(1)=0.186}$ , $\boldsymbol{\delta(2)=0.382}$ , $\boldsymbol{\delta(3)=0.176}$ , $\boldsymbol{\delta(4)=0.255}$

اکنون متغیر جدیدی به نام $a_i=\frac {A_i} N$ را معرفی می‌کنیم که برابر با نسبت هواپیماهایی که $i$ گلوله دریافت کرده‌اند به کل هواپیماهای شرکت کرده در عملیات است. سپس وایلد فرض کرد که اگر به طور مثال به یک هواپیما $n$ گلوله برخورد کند، این هواپیما قطعا سقوط خواهد کرد، بدین ترتیب درصد هواپیماهای سقوط کرده در صورتی که $i$ بزرگ‌تر از $n$ باشد که در حقیقت در این شرایط $a_i=0$ است برابر معادله زیر خواهد بود:

$\boldsymbol{L=1-\sum_{i=0}^{i=n}a_i}$

از مجموع تمام مقادیری که جمع‌آوری کرده‌ایم به دنبال این هستیم که $P_i$ را محاسبه کنیم. $P_i$ برابر با احتمال شرطی سقوط یک هواپیما پس از اصابت گلوله $i$ ام است به شرطی که به این هواپیما در گذشته $i-1$ گلوله اصابت کرده اما سقوط نکرده باشد.

اکنون با توجه به این موضوع متغیر $x_i$ را تعریف می‌کنیم. $x_i$ برابر درصد هواپیماهایی است که با اصابت گلوله $i$ ام سقوط کرده‌اند. بنابراین می‌توان گفت که $x_0=0$ است، یعنی اگر هواپیما مورد اصابت گلوله قرار نگرفته باشد، حتما بازخواهد گشت. بدین ترتیب مقدار $x_i$ یعنی کسری از هواپیماها که در اثر اصابت گلوله $i$ ام سقوط می‌کنند، از رابطه بازگشتی زیر بدست می‌آید:

$\boldsymbol{x_i={p_i}(1-{\sum_{j=0}^{i-1}a_j}-{\sum_{j=0}^{i-1}x_j})}$ , $\boldsymbol{i=1, 2, 3, ..., n}$

در نهایت با کمی بازی با روابط ریاضی، وایلد رابطه زیر را بدست آورد:

$\boldsymbol{{\sum_{j=0}^{n}\frac{a_j}{q_1 ... q_j}} = 1-a_0}$

در رابطه بالا $q_j$ برابر با احتمال آن است که هواپیما پس از اصابت گلوله $j$ ام سقوط نکند، به شرط آن‌که به هواپیما در گذشته $j-1$ گلوله اصابت کرده و سقوط نکرده باشد. در حقیقت می‌توان گفت:

$\boldsymbol{q_j=1-p_j}$

در ادامه برای اینکه بتوان یک حل عددی برای این مسئله در نظر گرفت، وایلد تصمیم گرفت چند فرضیه به مسئله اضافه کند تا کمک کند مسئله ساده‌تر حل شود. بنابراین او فرض کرد که $q_j=q$ و با این تصمیم مسئله را حل کرد. با اعمال این فرض، حل مسئله به شکل زیر خواهد بود:

$\boldsymbol{{\frac {a_1}{q}}+\boldsymbol{\frac {a_2}{q^2}}+\boldsymbol{\frac {a_3}{q^3}}+\boldsymbol{\frac {a_4}{q^4}}+\boldsymbol{\frac {a_5}{q^5}}\boldsymbol{= 1-a_0}}$

حال اگر اعداد را جای‌گذاری کنیم، خواهیم داشت:

$\boldsymbol{{\frac {0.08}{q}} +\boldsymbol{\frac {0.05}{q^2}} +\boldsymbol{\frac {0.01}{q^3}} +\boldsymbol{\frac {0.005}{q^4}} +\boldsymbol{\frac {0.005}{q^5}} \boldsymbol{= 0.2}}$

با حل این معادله خواهیم داشت:

$\boldsymbol{q=0.851}$

بنابراین با توجه به رابطه می‌توان نتیجه گرفت:

$\boldsymbol{p_i=0.149}$

اکنون با دانستن مقدار $p_i$ به راحتی می‌توان مقادیر مختلف $x_i$ را محاسبه کرد. بدین ترتیب خواهیم داشت:

$\boldsymbol{x_1=0.0298}$ , $\boldsymbol{x_2=0.01344}$ , $\boldsymbol{x_3=0.00399}$ , $\boldsymbol{x_4=0.00190}$ , $\boldsymbol{x_5=0.00087}$

البته در نظر داشته باشید که در این حالت ما در تمام حالات، $q_j$ را باهم مساوی گرفتیم و می‌دانیم که این فرض در واقعیت چندان صحیح نیست و با هر بار اصابت گلوله با هواپیما، احتمال بازگشت هواپیما کاهش می‌یابد. بنابراین واضح است که $q_j$ یک عامل محدود کننده است و باعث پیچیده شدن مسئله و غیرقابل حل شدن آن می‌شود.

در گام بعدی وایلد تصمیم گرفت که احتمال آسیب‌پذیری قسمت‌های مختلف هواپیما را محاسبه کند. همان‌طور که تعریف کرده بودیم، $\delta(i)$ برابر نسبت برخورد گلوله به قسمت $i$ به کل گلوله‌های اصابت شده است، به عبارت بهتر $\delta(i)$ برابر با احتمال این است که ناحیه $i$ مورد اصابت گلوله قرار گیرد. وایلد با انجام مجموعه‌ای از محاسبات توانست به رابطه زیر برای محاسبه $\delta(i)$ دست پیدا کند، به شرط آن که هواپیما تنها یک گلوله دریافت کند:

$\boldsymbol{\delta(i)={\frac {\gamma(i)q(i)}{\sum_{i=k}^{k}\gamma(i)q(i)}}}$

با کمی ساده‌سازی معادله بالا را می‌توان به شکل زیر نوشت:

$\boldsymbol{q(i)={\frac {\delta(i)q}{\gamma(i)}}}$

با داشتن مقادیر $\delta(i)$ و $\gamma(i)$ اکنون به راحتی می‌توان مقادیر $q_i$ را بدست آورد و محاسبه کرد که احتمال سالم بازگشتن یک هواپیما پس از برخورد گلوله با هر ناحیه چقدر است. با کمی محاسبه در نهایت خواهیم داشت:

با توجه به جدول فوق واضح است که موتور هواپیما آسیب‌پذیرترین قسمت هواپیما و احتمال بازگشت هواپیما پس از برخورد یک گلوله به آن ناحیه چیزی نزدیک به ۰.۵ است. بنابراین مطابق این جدول می‌توان تصمیم گرفت که کدام نواحی باید مقاوم سازی شوند.

اگر بخاطر داشته باشید، در ابتدای مقاله اشاره کردیم نظریه‌پردازان در ابتدا معتقد بودند که با توجه به تراکم اصابت گلوله‌ها باید بدنه هواپیما مقاوم‌سازی شود، اما با توجه به نتایج بدست آمده، واضح است که احتمال سالم بازگشتن هواپیما پس از برخورد گلوله به بدنه بسیار زیاد است و اصابت گلوله به این ناحیه خطر چندانی برای هواپیما و خلبان ایجاد نمی‌کند، در حالی که برخورد گلوله به موتور شانس زنده ماندن و بازگشت هواپیما را نصف می‌کند!

کلام آخر

همان‌طور که گفتیم، سوگیری بازماندگی می‌تواند با نادیده گرفتن شکست‌ها، باورهای خوش‌بینانه ایجاد کند. شما به عنوان یک مدیر محصول، چطور این سوگیری را تعریف و از آن پیشگیری می‌کنید؟

منابع:

$Mangel, M., & Samaniego, F. J. (1984). "Abraham Wald's Work on Aircraft Survivability." Journal of the American Statistical Association$

$Robert J Zimmer (2013-03-01). "The Myth of the Successful College Dropout". The Atlantic.$

نوشته شده توسط

جلیل علیزاده

دیدگاه شما الهام‌بخش است

No Comments

5 3 رای ها

امتیاز به این مطلب

اشتراک در

0 نظرات

بازخورد (Feedback) های اینلاین

مشاهده همه دیدگاه ها

فرصت‌های شغلی در تیم تکنولوژی

همه آنچه که باعث میشه دیجی‌کالا رو برای کار کردن دوست داشته باشی!